铁磁材料正被广泛应用于工业生产和人们的日常生活中，为保证材料及其制品在使用过程中的稳定性和耐久性，对材料进行性能测试尤为重要。铁磁材料的机械性能与其微观结构相关，通过改变材料的磁化状态进而改变材料内部的某些微观结构状态，使铁磁材料产生磁致伸缩效应。根据铁磁材料的磁滞现象，提出了一种基于磁滞回线的铁磁材料屈服强度分析方法。根据磁致伸缩EMAT接收端电磁超声信号幅值随发射端静态磁场改变而变化的特点，得到相应的静态磁感应强度-信号幅值蝶形曲线，并从中提取对铁磁材料的磁致伸缩特性较为敏感的特征参数。通过BP神经网络建立了磁致伸缩特征参数与材料屈服强度的映射关系，实现了对材料屈服强度的无损检测。

一、电磁超声基本理论

1.1  磁致伸缩现象与磁学理论

材料磁致伸缩行为的物理基础是铁磁性理论，磁致伸缩应变λ与磁场的关系有两种表述，其中一种是磁致伸缩滞后回线，如图1所示。当添加正向磁场时，λ随磁场的增加而增加；在退磁过程中，λ又随着磁场的减小而减小，由于剩磁现象两条曲线不重合，材料的λ有滞后，滞后回线滞后的大小与材料的矫顽力有关。当添加反向磁场时，其规律与正向磁场一致，具有对称性。图1所示为磁致伸缩材料的特性。

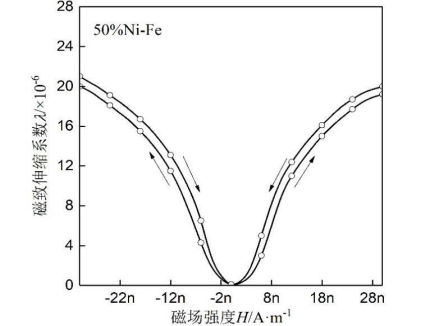
图1  50Ni-Fe软磁合金的磁滞伸缩滞后回线（n=79.6）

磁致伸缩滞后回线对材料的磁畴结构、畴壁运动难易程度都十分敏感。由于铁磁材料具有磁滞特性，在材料的反复磁化过程中，可以得到一条闭合磁化曲线，即磁滞回线，如图2所示。磁滞回线形成的原因也可以归纳为畴壁的位移和磁矩的转动。图中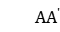为退磁曲线，由四部分组成：第Ⅰ部分是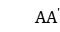，当磁场自A点减少到零时，每一个晶粒的磁矩都转动到该晶粒最靠近外磁场的易磁化方向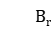，点对应的磁感应强度为剩余磁感应强度。在这个过程中，铁磁体内可产生新的反磁化畴。第Ⅱ部分是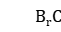，该阶段可能是磁畴磁矩的转动过程，也可能是畴壁的可逆位移，也可能有新的反磁化畴形成。第Ⅲ部分是CD，该阶段发生畴壁的不可逆位移。第Ⅳ部分是，它是磁矩转动到反磁化场方向的过程。整个过程中磁畴的运动，使得铁磁材料的长度或体积随之发生微小的变化，此微小形变的积累所导致的宏观形变，就是磁致伸缩发生的物理原因。当磁畴的元磁矩都转向外磁场方向并与外磁场平行时，可以认为磁致伸缩应变λ达到最大值。

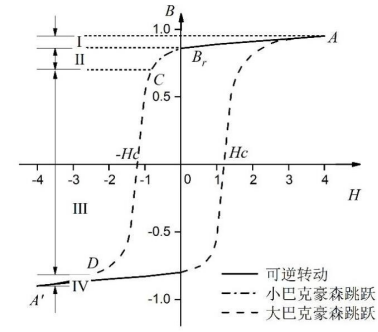
图2  退磁曲线与磁滞曲线

1.2  基于磁致伸缩机理的EMAT

铁磁性材料的磁致伸缩效应和逆磁致伸缩效应，是在铁磁性试样中激发和接收超声波的主要原理。 本文主要研究SH波信号的磁致伸缩特征参数与不同材料磁致伸缩特性的关系。外加静态磁场将被测样件磁化后，发射线圈通入高频大功率交变电流，根据电磁感应定理，铁磁性材料内部感生出同频电涡流，电涡流方向平行于静态磁场方向，同时线圈产生垂直于样件表面的动态磁场。由于铁磁性材料的磁致伸缩效应，被测试样会随着周期性变化的动态磁场在水平方向和竖直方向发生同频形变，产生磁致伸缩力，引发材料内部质点振动，激发出超声波。

由上面的理论分析可知，磁致伸缩效应的强度很大程度上取决于材料的微观结构特性以及应力状态。对于同种材料而言，通过检测磁致伸缩系数的变化，就可以检测出材料所受应力的变化。对于不同材料而言，通过检测磁致伸缩系数的变化，可以分析其内部微观特性的不同。因此，通过基于磁致伸缩效应的电磁超声检测方法对材料进行检测，能够获得反映材料的磁致伸缩特性曲线，图3反映了电磁超声信号幅值与磁致伸缩曲线的关系。

该图（b）中纵坐标代表电磁超声接收端信号幅值的大小。依据上下对比图可以发现，磁致伸缩曲线取得最大应变处，同时，在相同大小磁场强度磁化的条件下，接收端的超声信号会获得最小值。利用该理论现象，可以将电磁超声信号幅值与磁致伸缩效应相结合，通过选取合适的磁致伸缩特征参数来分析被测试件的机械特性。

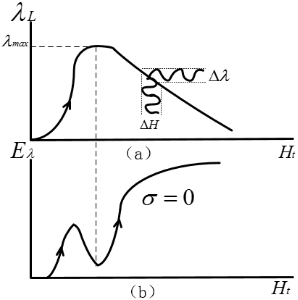
图3  磁致伸缩曲线与EMAT接收信号关系图

二、电磁超声检测平台

2.1  系统结构

完整EMAT系统如图4所示，由三个部分构成：超声激励端、EMAT换能器以及超声接收端。图中为完整EMAT系统结构框图。首先激励端产生高频激励信号，该信号被输入到发射线圈两端。高频猝发线圈在静态磁场的配合下，会在被测构件表面激发出一串同频振动信号。当超声波振动信号传到接收线圈处时，线圈会拾取微小的感应电动势，该电信号进入到模拟滤波放大电路后，通过数据采集卡被上位机获取，再进行一系列信号处理分析。

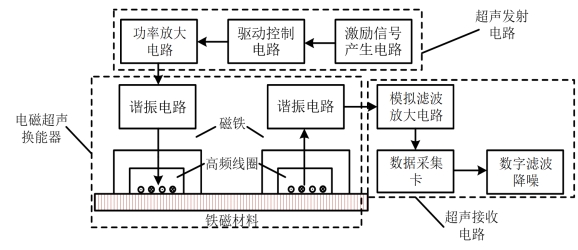
图4  电磁超声检测系统

2.2信号处理与特征提取

发射端采用可以调节磁场的交流电磁铁，通过改变电磁铁的磁场，采集对应磁场下的电磁超声接收端信号幅值，绘制出接收端电磁超声信号随发射端磁感应强度变化的曲线如图5，该曲线反映了材料的磁致伸缩特性。为了研究EMAT信号与铁磁性材料机械特性的关系，选取曲线中的交点、交点左右两个谷值以及四个峰值所对应磁感应强度作为特征参数。

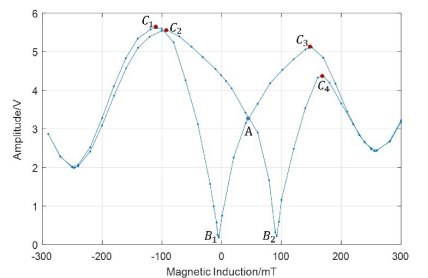
 图5  磁致伸缩特性曲线

三、实验结果与分析

本实验中采用样板尺寸为200*300mm的冷轧钢板作为实验试件，实验中对每一个样件重复测量五次。材料的屈服强度由同一批次标准试样通过离线拉伸试验获得，表1为材料参数。

表1 实验样件参数表               

3.1  特征值与屈服强度的关系

采用如下公式分析铁磁性材料磁致伸缩特征参数与铁磁性材料屈服强度的相关性：

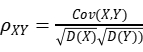                                     (1)

其中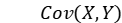表示变量X与变量Y的协方差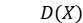，为变量X的方差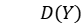，为变量Y的方差。

通过上述方法，得到各磁致伸缩特征参数与机械特性的相关系数如表2所示。

 表2 特征参数与屈服强度的相关系数

从表中可以看出信号的交点幅值A、第一峰值点磁感应强度C1、第四峰值点磁感应强度C4和两个谷值点磁感应强度B1、B2均与材料的屈服强度有较强的相关性。磁致伸缩特性曲线中，信号交点幅值大致随屈服强度的增大而减小；位于交点左侧的第一峰值点C1和第一谷值点B1的磁感应强度随屈服强度的增大而减小；位于交点右侧的第四峰值点C4和第二谷值点B2的磁感应强度随屈服强度的增大而增大。但是，特征参数随屈服强度的变化并不是单调的，因此需要建立更复杂的数学模型来映射特征参数与材料屈服强度的关系。

3.2  结合BP神经网络的数据结果分析

由于本次试验中对18个样本进行重复性测量5次，随机选取其中80%实验结果作训练样本。样本训练前，为了保证网络的收敛速度和网络性能，对72个测试样本和18个样本数据归一化。经过相关性分析，选出了5个相关度较强的磁致伸缩特征参数作为输入，输入层节点数为5，材料的屈服强度设置为输出参数，输出层节点数为1。隐含层节点数可由一下公式估算[1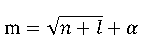2]：

(2)

其中m为隐含层神经元个数，n为输入层神经元个数，为输出层神经元数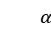，为1~10之间的常数。经过多次实验，最终确定隐含层节点数分别为9和7时，网络具有较高的精度。

经过500多次训练后，对屈服强度的预测值及相对误差如表3。

表3测试样本的屈服强度预测值

定义样件预测值与实际值的相对误差小于10%为预测合格，预测合格率来判断BP神经网络的精度，从表1中可以看出对屈服强度的预测合格率达94.44%,因此通过该BP神经网络模型对铁磁性材料的屈服强度预测，可以达到90%以上的合格率。结果表明，结合神经网络，可以通过磁滞回环下多个基于电磁超声特性的参数测量铁磁性材料机械特性。